
Disclaimer: Everything here might be wrong. Feel free to correct me if you believe it so.
Let’s say you wanted to create a solenoid strong enough to levitate at the poles of the Earth’s magnetic field, and thus, the first skate truck for a true hoverboard. How practical would that be?
First, let’s use Lenz’s Law as an approximation for the solenoid. We are able to treat our solenoid as a long wire, as the magnetic field is going to be uniform in X, Y, and Z for the recommended use case of a hoverboard.
Force = Current * Length x B-Field
Assuming we want to levitate a 1kg, 100m long solenoid coil in the uniform earth magnetic field…
F = 9.8 Newtons
L = 100 meters
B = 50 uTesla
(9.8 N) = I * (100 m) * (0.00005 T)
I = 1960 Amperes
Thus we need a current of 1960A running in our solenoid to generate this field.
Naturally, this is impossible with copper wire. However, plasma is extremely conductive, so perhaps we could create a long glass tube using a fiber-optic manufacturing process. Then we must ask, what are the resistive losses in a coil of 1keV plasma?
Let’s use a simplified version of Spitzer Resistivity to find an approximate specific resistance:
n = 5.15 * 10^(-5) * (0.993 * 10) / ((1000)^(3/2))
n = 1.617 * 10^-8 ohm/m
Then use ohm’s law to find the coil’s losses:
P = I^2 * R
P = (1960 A)^2 * (1.617 * 10^-8 ohm/m) * (100 m)
P = 6.212 W
Despite the high current, our resisitve losses for this plasma are relatively low at only 6.2 Watts!
Now, how much plasma really is this? We can get an approximation by assuming a unit charge per molecule. A current of one Ampere is equal to 1 coulomb per second, which is approximately 6.25 x 10^18 elemental charges passing by per second. We can use Avogadro’s number to make sense of this.
(1960 A) * (6.25 x 10^18 charges/coulomb) = (1.55 * 10^22 charges/s)
1.55 * 10^22 / Avagadro’s Number = 0.02034 mols
Assuming our plasma is Xenon with a molar mass of 131 grams we find, that’s only 2.6 grams of xenon.
2.6 g == 0.02034 mol * 131 g / mol
At standard temperature and pressure, that’s less than 1 liter of xenon.
Seems like not too much?
Questions for the reader:
What other losses are not taken into account?
What is the power needed to maintain the 1000eV plasma temperature in the 100 meter tube?
What would the mass of a 100 meter glass tube be, to maintain the structural integrity needed to contain the plasma?
Responses are welcome :-)

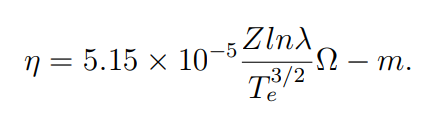
Scientist Smith YT
The 1,960 amps can be sustained in copper wire. I’ve ran 3,000 amps through 0 gauge stranded copper wire in an electromagnet. Generating a real flux of 11, 400 gausses. Yet, to repel that much force towards the earth magnetic field. That wouldn’t work. You would still be on the ground.
This is going to be long so stay awake…
One thing the formulas dont take into consideration is the voltage. I used 3,000 amps at 12 volts. But am still on the ground. The coil doesn’t even lift up. It only weighs 10 pounds. The massive amount of electricity needed would be …. One sec… Math here and math there equals 1.02859528E15 watts. So about 37553728.3001212121 volts and 27389964.2001 amps. But that’s might not be enough to be stable. As far as floating goes. Your magnetic field will be approximately 104,081,864 Gauss or 10,408.1864 Tesla.
To put it to perspective that much energy can be produced by at best approximately by 5 or so power plants. If you want to lift off the ground with some stability. It would be… Let me do some more math….
Got it!
That’s…
Amps: 73,039,904.53
Volts: 100,143,275.50
Watts: 7.31445549E5
To give a perspective on that it would need…
35 and a half power plants to power this device.
For magnetic flux it is…
Gauss: 740,137,656.60
Tesla: 74,013.76566
IMPORTANT NOTES:
This is based on my real life measurements. The smaller amperages and voltages of course. No one including me has enough power like this. I did some math off of my experiment and these are the mathematical real life values. This is the closest you can get to real life values with magnetic field strength. I am very careful myself to use the laws relating to flux density and lift/pull force. They are EXTREMELY rough estimates amd can be way far off from the real values. As you have seen already in this post.
Thanks, From The Magnet Nerd Himself.